Choques en dos dimensiones
Ya hemos visto que la cantidad de movimiento de un sistema es constante cuando el sistema está aislado. Para cualquier colisión de dos partículas en el plano, este resultado implica que la cantidad de movimiento en cada una de las direcciones X e Y es constante.
El juego de billar es un ejemplo muy familiar en el que se producen múltiples choques entre partículas en dos dimensiones. Para este caso las ecuaciones de la conservación de la cantidad de movimiento para cada eje son:
|
Conservación de la cantidad de movimiento |
|
| En el eje X | $ m_1 \cdot v_{1xi} + m_2 \cdot v_{2xi} = m_1 \cdot v_{1xf} + m_2 \cdot v_{2xf} $ |
| En el eje Y | $m_1 \cdot v_{1yi} + m_2 \cdot v_{2yi} = m_1 \cdot v_{1yf} + m_2 \cdot v_{2yf} $ |
A la hora de resolver problemas debes sustituir los valores conocidos y resolver este sistema de ecuaciones.
Vamos a considerar el caso de un choque en dos direcciones en el que una partícula de masa m1 choca con otra de masa m2 que está inicialmente en reposo.
Después de la colisión, la bola 1 se mueve con un ángulo $\alpha$ respecto a la horizontal y la bola 2 se mueve con un ángulo $\beta$ con respecto a la horizontal. En el siguiente esquema puedes ver la situación antes y después del choque:
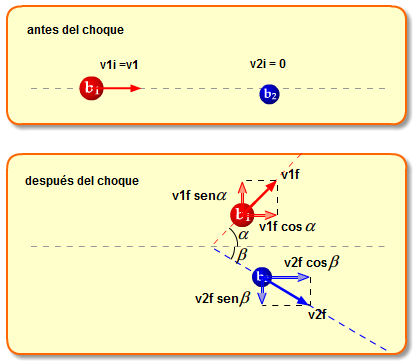
Si aplicamos la ley de conservación del momento a cada eje, y teniendo en cuenta que la cantidad de movimiento inicial de la bola 2 es cero, tenemos:
Conservación de la cantidad de movimiento
pantes = pdespués |
|
| En el eje X | $m_1 \cdot v_{1i} = m_1 \cdot v_{1f} \cdot cos\alpha + m_2 \cdot v_{2f} \cdot cos\beta$
|
| En el eje Y | $0 = m_1 \cdot v_{1f} \cdot sen\alpha + m_{2} \cdot v_{2f} \cdot sen\beta$ |
Vamos a resolver un caso concreto para que aprendas cómo se monta este sistema de ecuaciones y cómo se resuelve: