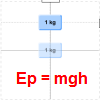





En el simulador se muestra un cuerpo de 1 kg de masa situado en la cercanía de la superficie terrestre, en la que la gravedad es $g = 9.8 m \cdot s^{-2}$ (o bien $g = 9.8 N/kg$)
Para bajas altitudes el peso de un cuerpo es constante.
Observa que para desplazamientos horizontales el trabajo realizado es cero porque la fuerza gravitatoria (el peso del cuerpo) y el desplazamiento son perpendiculares entre sí: $$Wg (desplazamiento_{horizontal}) = 0$$
Si el desplazamiento es vertical podemos usar la ecuación genérica $W = F_{y}Δh$.
En nuestro caso la fuerza es el peso del objeto y la dirección positiva del eje Y es hacia arriba (opuesta a ⃗g) luego:
$$W_g = (- mg) Δh$$ $$W_g = −mgΔh $$ $$W_g = −mg (h_2 - h_1) $$ $$W_g = mgh_1 - mgh_2$$Esta ecuación la solemos expresar como
$$W_g = − ΔEp_g$$La ecuación anterior tiene validez general es decir, se puede aplicar a cualquier movimiento curvilíneo.
También se deduce de la ecuación que el trabajo de peso es independiente del camino y depende solo de las posiciones inicial y final.
Las fuerzas para las cuales su trabajo es independiente del camino y depende solo de la fuerza y las posiciones inicial y final se denominan fuerzas conservativas.
Puedes mover el cuerpo y el suelo para cambiar la situación del nivel cero de energía potencial.
Etiquetas: Bachillerato energía HTML5 trabajo
