Mueve el deslizador de temperatura hacia atrás y hacia adelante y observa las partículas. ¿Qué aprecias en el movimiento de éstas?

La temperatura de una sustancia es una medida de la energía cinética media de sus partículas (la energía cinética es la energía del movimiento). La energía cinética (Ec) de una partícula es igual a su masa multiplicada por el cuadrado de su velocidad, dividida por dos:

$$Ec =\frac{1}{2} m\cdot v^2$$

• De acuerdo con la ecuación de la energía cinética, ¿cómo cambiará la temperatura si aumenta la velocidad media de las moléculas en un gas?
• ¿Cómo cambiará la temperatura si aumenta la masa de las moléculas de gas?

- Las moléculas de oxígeno tienen 16 veces más masa que las de hidrógeno. A la misma temperatura ¿cuáles crees que se moverán más rápido?Compruébalo con el simulador.

- Basándote en la definición de temperatura, explica por qué las moléculas de oxígeno se mueven más lentamente que las de hidrógeno a la misma temperatura.

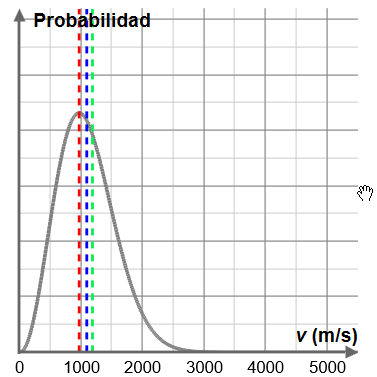
La gráfica representa la distribución de Maxwell-Boltzmann de las velocidades de las partículas. La curva representa la probabilidad de que una partícula se mueva a la velocidad que se muestra en el eje x de la gráfica. Cuanto más alta sea la curva, mayor será la probabilidad de encontrar una partícula que se mueva a esa velocidad.

- Mueve el deslizador de temperatura hacia atrás y hacia adelante y observa la gráfica de la derecha. ¿Qué observas sobre la forma de ésta?

- Selecciona el gas hidrógeno y observa el lado izquierdo de la gráfica a medida que elevas la temperatura de 50 a 1.000 K.

• Incluso a las temperaturas más altas, ¿todavía hay algunas partículas lentas?
• ¿A qué temperatura ves la mayor variedad de velocidades de partículas?
• En general, ¿la curva de Maxwell-Boltzmann es una curva simétrica o asimétrica?

Como las partículas tienen un rango de velocidades a cualquier temperatura dada, es útil calcular la velocidad promedio. Los físicos expresan la velocidad promedio de tres maneras:

la velocidad más probable ($v_p$)
la velocidad media ($\overline v$)
la velocidad cuadrática media ($v_{rms}$).

- Selecciona gas hidrógeno a la temperatura de 200 K

• Estima la velocidad más probable observando el pico de la curva. ¿Cuál es tu estimación?
• Marca “Ver velocidad más probable”. ¿Cuál es su valor?
• Basándote en la forma de la curva, ¿crees que la mayor parte de las partículas se mueven más rápido o más lento que la velocidad más probable?

- La velocidad media es la media de las velocidades de todas las partículas. Basándote en la forma de la curva y en tu respuesta anterior, se puede esperar que la velocidad media sea mayor o menor que la velocidad más probable? Explica tu razonamiento.

- Marca “Ver velocidad media”. ¿Qué valor tiene?¿Fue correcta tu predicción?

- Eperimenta con otros gases y temperaturas. ¿Es la velocidad media siempre superior a la velocidad más probable? Intenta explicar porqué es así.

- Ahora desmarca todas las casillas y seleciona has hidrógeno a la temperatura de 100 K. Puedes calcular la velocidad más probable ($v_p$), la velocidad media ($\overline v$), y la velocidad cuadrática media ($v_{rms}$) con las siguientes ecuaciones:

$$v_p = \sqrt \frac{2RT}{M}$$ $$\overline v = \sqrt \frac{8RT}{\pi M}$$ $$v_{rms} = \sqrt \frac{3RT}{M}$$

En estas ecuaciones:

• R es la constante universal de los gases y tiene un valor de $8.3144 \frac{J}{K \cdot mol}$
• T representa la temperatura Kelvin
• M representa la masa molar, en kg/mol

Es importante señalar que la energía cinética media que se utiliza aquí, se limita a la energía cinética de traslación de las moléculas. Es decir, las moléculas son tratadas como masas puntuales y no se tienen en cuenta los grados de libertad internos, tales como la rotación molecular y la vibración.

- Sabiendo que la masa molecular del hidrógeno es 0.002016 kg/mol, calcula las tres velocidades y luego comprueba tus resultados.