En un triángulo rectángulo la tangente del ángulo $\alpha$ es el cociente entre el cateto opuesto y el cateto contiguo: $$\text{tan} \alpha =\frac{ \text{cateto opuesto} }{\text{cateto contiguo}}$$

Si usamos como referencia la imagen anterior tendríamos: $\text{tan} \alpha =\frac{y}{x}$

 

Recuerda que si trabajamos con el círculo unitario el cateto opuesto coincide con el seno del ángulo y el cateto contiguo coincide con el coseno por lo tanto: $$\text{tan} \alpha =\frac{ \text{sen} \alpha} {\text{cos} \alpha}$$

Vamos a arrastrar el punto alrededor del círculo, de 0° a 360°, en dirección contraria a las agujas del reloj

Contesta a las siguientes preguntas sin usar el simulador:

• tan α = 0 cuando α = ?
• tan α es indefinida cuando α = ?
• tan α = 1 cuando α = ?
• tan α = –1 cuando α = ?
• ¿En qué cuadrantes es positiva la tan α?
• ¿En qué cuadrantes es negativa la tan α?

Ahora comprueba tus predicciones con el simulador.

Mueve el punto alrededor del círculo dando lentamente varias vueltas completas

• ¿Con qué frecuencia se repiten los valores de tan α?

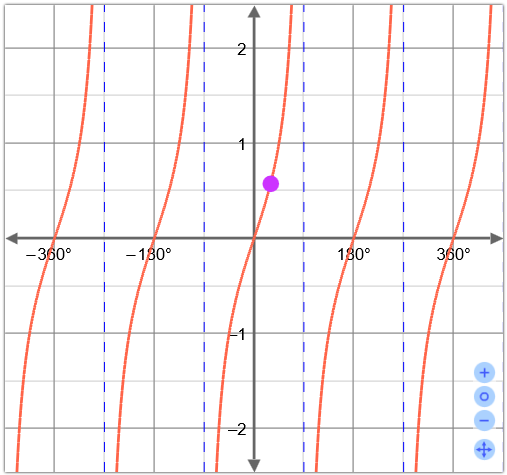
Habrás encontrado que la tan α se repite cada 180°. Este intervalo es el periodo de la función tangente. Una función que se repite a intervalos regulares, como en nuestro caso, es periódica.

Observa que la función tangente no está definida cuando cos α = 0 . Por lo tanto, la función tangente tiene una asíntota vertical donde cos α = 0. Estas asíntotas verticales son las líneas de segmentos azules que aparecen en la gráfica.

 

[texto en construcción]

---