Si hemos acordado llamar movimiento al cambio de la posición con el tiempo, será necesario establecer un criterio para determinar qué posición ocupa un cuerpo en un instante.

Se trata, de nuevo, de establecer un sistema de referencia adecuado para lo que necesitamos estudiar.

Una dimensión

Imagina que tenemos un cuerpo que se mueve por una recta, es decir que realiza un movimiento en una dimensión. Para determinar su posición sólo necesitamos indicar a qué distancia del origen se encuentra. Observa en el siguiente applet que la posición del cuerpo puede ser positiva o negativa según se encuentre a la derecha o a la izquierda del orígen respectivamente.

Representa en el applet anterior los siguientes puntos:

• P(2.8)
• P(-1.6)
• P(0)

Como ves resulta muy fácil hacerlo. Con una coordenada podemos conocer la posición de un punto sobre una recta.

Dos dimensiones

Si el cuerpo realiza un movimiento en dos dimensiones, es decir se mueve por un plano, necesitaremos dos coordenadas para determinar la posición que ocupa en un instante dado.

Los dos valores que determinan la posición de un cuerpo en un plano podemos establecerlos utilizando como referencia un sistema de coordenadas cartesianas o un sistema de coordenadas polares.

En el caso de las coordenadas cartesianas se utilizan las distancias a los dos ejes acompañadas de los signos (+) ó (-).

En la figura de la izquierda aparece representado el punto P(3,2). Para evitar confusiones se tiene el acuerdo de escribir primero la coordenada x y después la coordenada y, separadas por una coma.

El signo negativo para la coordenada x se utiliza si el punto se encuentra a la izquierda del orígen y para la coordenada y cuando está por debajo del orígen.

Las coordenadas polares utilizan la longitud de la recta que une nuestro punto con el punto de referencia y el ángulo que forma esta recta con la horizontal.

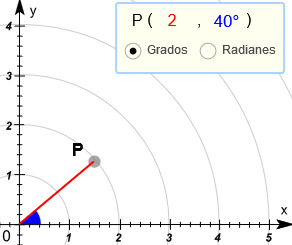En la figura de la izquierda se representa el punto P(3 , 45°), que significa que la distancia OP vale 3 y que el ángulo vale 45°

En el siguiente applet puedes representar los puntos dados en:

C. Cartesianas	C. Polares
(-1.3, 2) (-2, -2) (0, 1.8) (2.4, 0) (0.7, 1.5)	(3, 45°) (2, 160°) (3, -90°) (2, 30°) (1, 90°)

Tres dimensiones

En el caso de un cuerpo que siguiera una trayectoria de tres dimensiones, necesitaríamos tres coordenadas para determinar su posición en un instante dado.

También en este caso se pueden utilizar coordenadas polares y coordenadas cartesianas. En el siguiente applet puedes ver un sistemas de ejes cartesianos tridimensional:

 

El tiempo es la cuarta dimensión

Como el movimiento es el cambio de la posición con el tiempo, además de conocer la posición, nos interesa saber el instante en el que el cuerpo ocupa dicha posición.

Si representamos el conjunto de las diferentes posiciones que ocupa un móvil a lo largo del tiempo, obtenemos un línea llamada trayectoria.